Tit for tat is an age-old proverb which we have heard since childhood. But let’s try to mathematically prove its effectiveness.
Game Theory
Any scenario where there are two or more “players” with ability to think and which involves some payoffs can be treated as a game.
Game theory studies how these players interact with each other. If you loan a bowl of sugar to your neighbor, do they return the favor or exploit your kindness. If the Khaleesi launches a dragon attack on King’s Landing, will King’s Landing retaliate with a nuclear attack? Game theory explores these scenarios.
It's a great way to understand strategy and decision making in all aspects of life, from personal decisions to decisions at national level.
Prisoner’s Dilemma
To understand it better, we take a classic thought experiment from game theory called Prisoner’s Dilemma.
This game can be formulated or described in many ways, but the basic structure of the game is that there are two prisoners. Let's call them A and B. Both are accused of some crime. Now, both prisoners are taken into separate rooms and questioned.
Neither A, nor B knows how the other one is going to act. They can choose to cooperate or defect. Based on how they choose to act, the prisoners will get Payoffs.
Now the payoff could be reduced sentence for cooperation with the police or defection against the other prisoner. But let’s consider it to be points for simplicity.
Here’s a representation of the game in form of (points for A, points for B) in each scenario:
The dilemma for prisoners is to choose whether to defect or to cooperate.
One-shot
Of course, the best outcome for both players in this case will be if both choose to cooperate.
But what if the other person defects, in that case you will be stuck with zero points while the other person gets all the rewards.
But if you defect, and the other person cooperates, you get all the reward.
Therefore, no matter what, the dominant Strategy seems to be, to always defect.
If your opponent is rational, they will also reach the same conclusion and always defect.
In such cases, both agents are stuck with the suboptimal reward 1-1, where they could both have gotten 3-3 each if they chose to cooperate.
Series
Most real-world problems are not a single prisoner's dilemma. It's a series of such games. If you defect and your opponent cooperates for the first time, your opponent will know you defected last time and that can change their behavior. You have to be long-sighted when deciding your strategy.
In 1980, Robert Axelrod hosted a computer competition to determine this. He pitted multiple computer programs based on different strategies against each other in a series of Prisoner’s Dilemma. Here are some of the participating strategies:
Friedman: It starts by cooperating, but if its opponent defects even once, it defects for the rest of the game.
Joss: It starts by cooperating and copies what its opponent did in the last move. It also sneaks in a defection 10% of the time.
Graaskamp: Same as Joss but it defects on the 50% round.
Tit-for-tat: Starts by cooperating and copies what its opponent did in the last move. No random or probabilistic defections.
Effectiveness of TFT
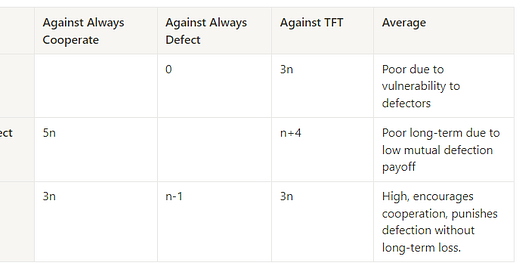
To assess the effectiveness of tit-for-tat, let’s compare it with two extreme strategies of ‘always defect’ and ‘always cooperate’ and against itself.
Let the respective payoffs for always-cooperate, always-defect and tit-for-tat be:
Case 1: TFT vs. Always Cooperate
When Tit for Tat plays against a strategy that always cooperates:
Both players always cooperate after the first round.
Payoff per round: (3, 3)
Over n rounds:
\(P_{TFT}=P_C = 3n\)
Case 2: TFT vs. Always Defect
When Tit for Tat plays against a strategy that always defects:
Round 1: TFT cooperates, opponent defects. Payoff: (0, 5)
Subsequent rounds: Both defect. Payoff per round: (1, 1)
Over n rounds:
\(P_{TFT}=0+1(n−1)=n−1\)
Case 3: TFT vs. TFT
When Tit for Tat plays against another Tit for Tat:
Both players always cooperate after the first round.
Payoff per round: (3, 3)
Over n rounds:
\(P_{TFT}=3n\)
Comparing the averages:
Any guesses on which strategy won Axelrod’s competition? Although, it seemed like the craziest thing at the time, the simplest strategy ended up winning, there’s a reason tit-for-tat does so good against all strategies.
Defecting strategies like Always defect, seemed to be good strategy in one-shot to get a payout of 5 over your opponent’s 0. But when both parties always defect, they end up getting lower payout of (1,1), which isn’t good for either of them.
Always cooperate would be great in an ideal world, with both players winning (3,3), but it performs poorly due to the fact that there can be nasty players who will sneak in a defection and even continue to do so if they see cooperation from the other side. Always cooperate is overly nice.
TFT is at the sweet spot, where its nice enough to cooperate first, but it punishes the opponent in the next round if they defect. However, it doesn’t keep defecting, it forgives the opponent as soon as they get back to cooperating and they both get a higher payout of (3,3) instead of (1,1).
Axelrod found that all the best performing strategies shared these qualities:
They’re nice: They start with cooperation, setting a precedence for a positive, cooperative relationship.
They’re provokable: They mimic the opponent's previous move, directly punishing defection and rewarding cooperation, fostering a stable environment where mutual cooperation can thrive.
They’re forgiving: They don't hold grudges and only respond to the last move. A player who defects once and then returns to cooperation will be met with cooperation, preventing a downward spiral of mutual defection.
There is a misconception that TFT can never do better than its opponent.
By design, TFT can only loose or at best have a draw with its opponent.
On the other hand, the "Always deflect" strategy will always draw or win.
While this is true in a one-on-one game series with a single opponent, most of life is not like that. When there are multiple agents involved with different strategies and different noises at play, the results are totally different. When most people think of games, or in general anything in life, they think someone has to lose in order for them to win. But that’s not the case with Prisoner’s Dilemma and certainly not the case in real life.
In such games, winning is not as important as securing the greatest number of points. Since you are not getting your reward from the other player, but from a third-party. And TFT eventually ends up gaining most points even by just drawing most games. With mutual cooperation we can ensure a win-win outcome for everyone. Tit-for-tat does exactly that.